Tools
Guides
Resources
About
Tools
Guides
Resources
About
📝 You can now participate in the second anniversary survey here!
WURMPLE EVOLUTION
-Calculator-
Wurmple's evolution is determined by its personality identification number prior to generation 6, which is generated during the moment it appears in the wild or as an egg, but there is no way inside the games to know this value, nor into which Pokémon Wurmple will evolve before actually evolving it. Doing so won't take much time, as it barely needs a few levels, but if you somehow know the PID of a Wurmple (or multiple), you can use this calculator to know which evolution you will get. If you're interested in the calculations behind this phenomenon, this page also contains an in-depth explanation.
-Explanation-
To explain the process of calculating a Wurmple’s evolution, I will use these four Wurmples as an example.
| PID | Level | Nature | Gender | |
|---|---|---|---|---|
| Wurmple 1 | AE753E11 | 4 | Timid | Female |
| Wurmple 2 | 45814C59 | 4 | Bashful | Female |
| Wurmple 3 | BD5B7C5 | 3 | Naive | Male |
| Wurmple 4 | 59DC9190 | 3 | Impish | Male |
A Pokémon’s PID is composed by 32 bits, represented in hexadecimal. These bits can have one of two values, 0 and 1. The 16 high bits are used to determine a Wurmple’s evolution. An easy way to see this, is by converting it to binary, so we can take a closer look at each part:
AE753E11 → 10101110011101010011111000010001
The 16 high bits are highlighted
| PID (hex) | PID (binary) | |
|---|---|---|
| Wurmple 1 | AE753E11 | 10101110011101010011111000010001 |
| Wurmple 2 | 45814C59 | 01000101100000010100110001011001 |
| Wurmple 3 | BD5B7C5 | 00001011110101011011011111000101 |
| Wurmple 4 | 59DC9190 | 01011001110111001001000110010000 |
Let’s also convert these binary numbers to decimal notation, for future convenience. So our list of Wurmples and their 16 high bits would look like this:
| PID's high 16 bits (binary) | PID's high 16 bits (decimal) | |
|---|---|---|
| Wurmple 1 | 1010111001110101 | 44661 |
| Wurmple 2 | 0100010110000001 | 17793 |
| Wurmple 3 | 0000101111010101 | 3029 |
| Wurmple 4 | 0101100111011100 | 23004 |
The next step will be dividing each value by 10, which we converted to decimal notation before, so it will be easier to calculate. But here’s the thing: we are not looking for the result of the division, the value we’re looking for is the remainder. So, for example, if we calculate the first Wurmple, 44661 / 10, the result will be 4466 (without decimals), but the remainder will be 1, which is what we’re interested in. We can also use modulo to get this number directly (44661 % 10 = 1).
This is the value that changes everything. Wurmple will evolve into Silcoon when this number is less than 5 (5 not included). Wurmple will evolve into Cascoon when this number is 5 or more (5 included). This is how our final Wurmple list will end like:
| Calculation | Result | Expected evolution | |
|---|---|---|---|
| Wurmple 1 | 44661 % 10 | 1 | Silcoon |
| Wurmple 2 | 17793 % 10 | 3 | Silcoon |
| Wurmple 3 | 3029 % 10 | 9 | Cascoon |
| Wurmple 4 | 23004 % 10 | 4 | Silcoon |
And here are our Wurmples before and after evolution:
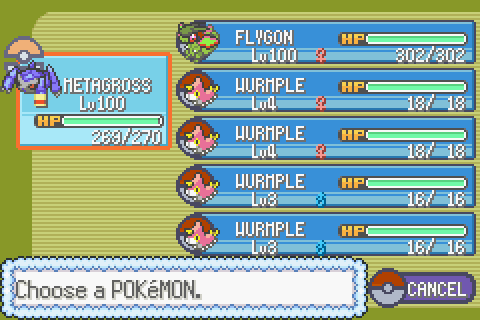
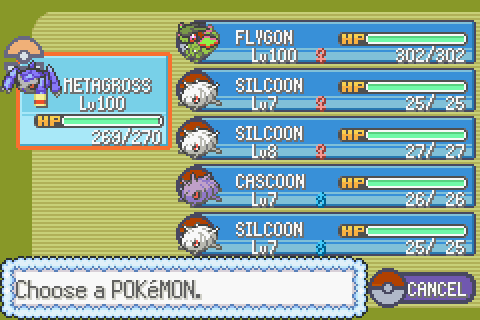
Basic math also tell us that our remainder can’t be greater than the divisor (10 in this case), so there will be five results for Silcoon (0, 1, 2, 3, and 4) and five for Cascoon (5, 6, 7, 8, and 9), making the choice of evolution as close as possible to a 50/50 chance (taking the limitations of the game’s pseudo-randomness aside).